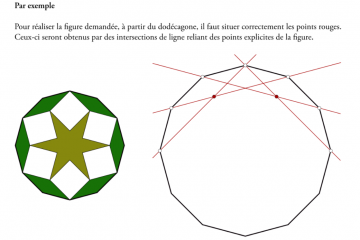
Les découpeuses numériques ont leurs logiciels spécifiques permettant de créer des modèles vectoriels 2D avec des contraintes afin qu’ils soient découpables. Cela dit, ces logiciels acceptent la plupart du temps l’importation de fichiers au format SVG (Scalable Vector Graphic) conçus, par programmation ou à l’aide de logiciels de géométrie, en respectant ces mêmes contraintes.
En collège comme en lycée, pour la géométrie plane dynamique en mathématiques, les élèves et les professeurs utilisent de plus en plus GeoGebra. Ce logiciel permet de concevoir des modèles exportables en SVG en vue de leur découpe numérique à lame ou laser.
La découpe numérique est alors accessible à tous dès le cycle 3. Elle permet une découpe précise de patrons divers dans des matériaux très variés. Dans l’article tutoriel qui suit, la découpeuse Silhouette CAMEO 4 est utilisée pour découper, dans du papier cartonné, des patrons, avec ou sans colle, en couleur ou non, d’une stella octangula et de sa fractale.
Coup d’œil
- On aime :
- Le logiciel GeoGebra classic 5 pour réaliser un modèle 2D et l’exporter au format SVG dans le but de sa découpe par une découpeuse numérique, ici la Silhouette CAMEO 4 (format A3 et +) avec le logiciel Silhouette Studio Designer ou Business edition. Les longueurs sont conservées.
Informations
Nécessite une installation :
Le logiciel de la découpeuse : Silhouette Studio (designer edition ou business edition) et la version classique 5 de GeoGebra.
Nécessite une connexion Internet :
Pour télécharger les logiciels et applications.
Disponibilité (système) :
Windows/IOS selon les logiciels.
Prix :
La découpeuse numérique à lame Silhouette CAMEO 4 permet une découpe de 30 cm environ de large et coûte environ 300 euros. D’autres modèles de découpeuses de la même marque sont aussi sur le marché : Silhouette Portrait (jusqu’au format A4 à environ 200 euros), Silhouette CAMEO 4 Plus (avec une dimension de découpe de 37 cm de large à environ 400 euros) et Silhouette CAMEO 4 pro (avec une dimension de découpe de 60 cm de large à environ 550 euros).
Une extension du logiciel de la découpeuse afin de pouvoir importer des fichiers SVG peut être payante (environ 50 à 100 euros selon la version).
Matériel :
Ordinateur, découpeuse Cameo 4, tapis de transport 12 in x 24 in (30 cm x 60 cm), feuilles A3 et A4 de papier cartonné 160g/m² ou 350 g/m².
Imprimante couleur (A3 si possible) pour les patrons en couleur.
Utilisation
Dans les sections ci-après, un tutoriel décompose par étapes des procédures à suivre pour : concevoir, avec GeoGebra classic 5, un modèle 2D (patron) d’un solide mathématique, celui d’une stella octangula, l’exporter en SVG et l’importer dans le logiciel spécifique Silhouette Studio Business edition de la découpeuse numérique à lame : la Silouhette CAMEO 4.
Grâce à des outils GeoGebra proposés ici, ce patron en papier cartonné pourra être assemblé sans colle ni adhésif.
Le solide mathématique stella octangula a été choisi d’une part parce que sa modélisation 3D en vue de son impression 3D a déjà été expliquée sur ce même site et d’autre part parce qu’ayant la possibilité de réaliser le modèle 2D de différentes façons, il y a un intérêt à son intégration dans un projet mathématique (non détaillé ici) à mettre en œuvre au cycle 4 idéalement en classe de 4ème (suggestion : parcours artistique et culturel).
Il sera également décrit comment réaliser un patron (sans colle ni adhésif) de la fractale de tétraèdres stella octangula (jusqu’à l’itération 3 voire 4) en plusieurs morceaux.
Pour finir, le « Comment mettre les patrons en couleur ? » sera détaillé.
1. Paramétrer GeoGebra classic 5
1. Paramétrer GeoGebra classic 5
A l’ouverture de GeoGebra classic 5, choisir « Géométrie ».
1.1. INTEGRER DES OUTILS LANGUETTES
Afin de pouvoir bénéficier des outils GeoGebra permettant de créer des languettes automatiques, télécharger le fichier ZIP ci-joint, le dézipper et ouvrir à partir de GeoGebra classic 5 le fichier au format ggt nommé art3d-clb-outils-languettes-decoupeuse-v2021.ggt ou bien glisser le fichier sur la fenêtre ouverte de GeoGebra classic 5.
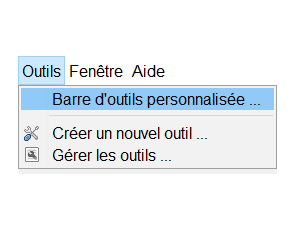
Afin d’appeler ces outils dans la barre d’outils, cliquer sur l’onglet « Outils » puis « Barre d’outils personnalisée ».
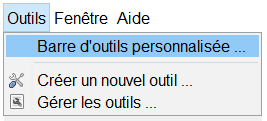
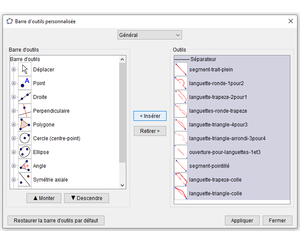
Pour personnaliser, votre barre d’outils, sélectionner les outils de la colonne de droite pour les insérer dans celle de gauche.
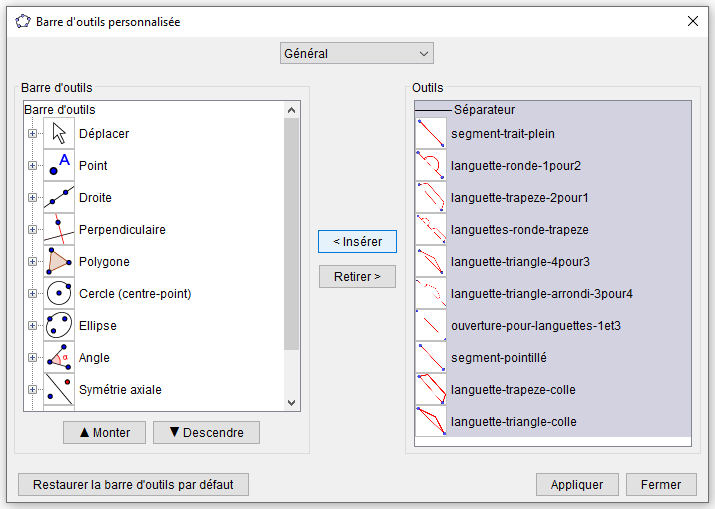
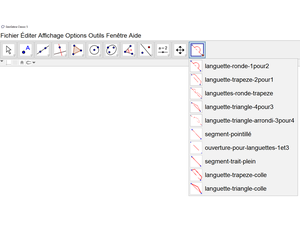
Vous pouvez choisir la place de chacun des outils si vous le souhaitez. Vos outils languettes apparaîtront dans votre barre d’outils, désormais personnalisée :
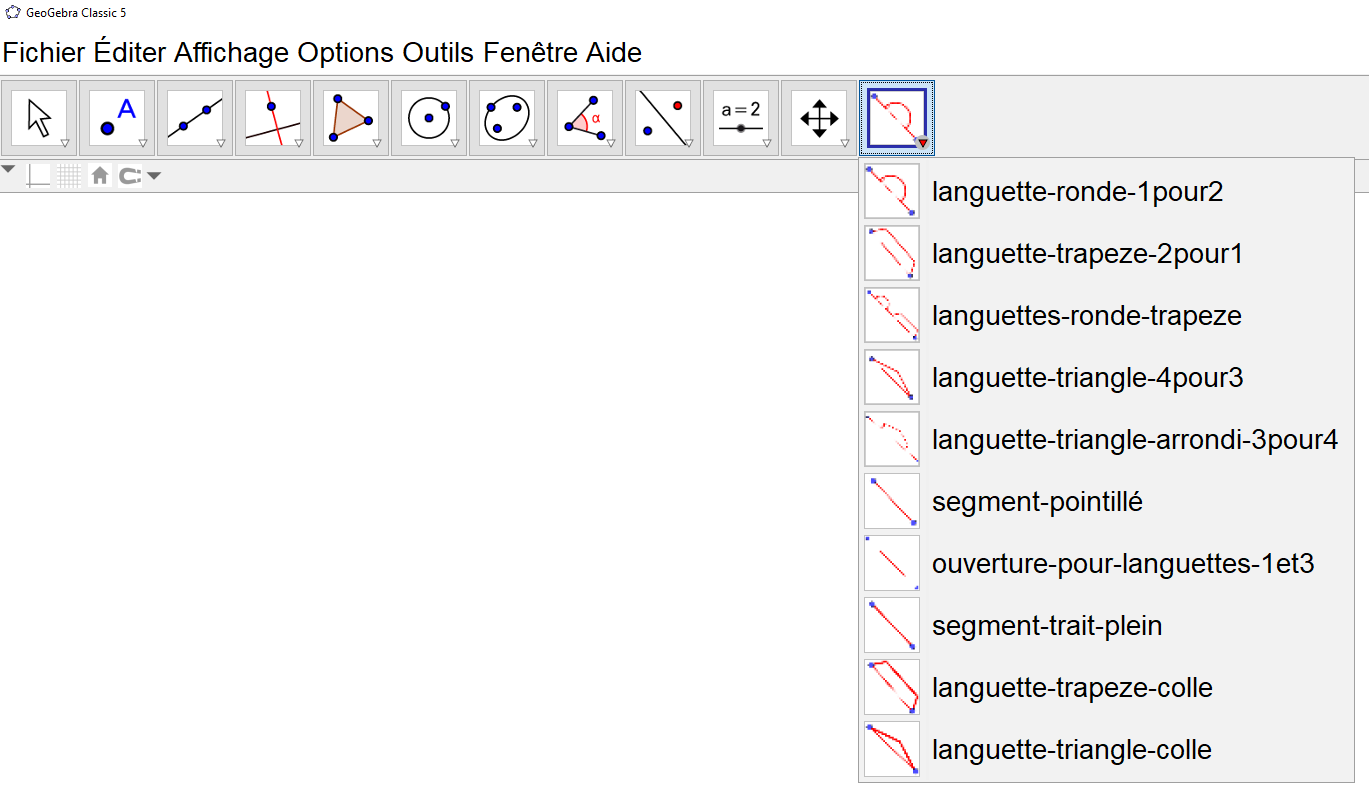
Puis, si ce n’est pas déjà le cas, cacher les axes et le quadrillage afin d’avoir une fenêtre (plan) blanche (blanc).
1.2. INTEGRER UN CURSEUR pour la longueur d’une arête variable
Afin de pouvoir modifier facilement les dimensions de la stella octangula d’arête de 1 cm à 11,8 cm par exemple, créer un curseur de 0.5 à 5.9. Celui-ci pourra être modifié par la suite si nécessaire.
Pour se faire, cliquer sur l’icône « Créer curseur » puis cliquer dans le plan.
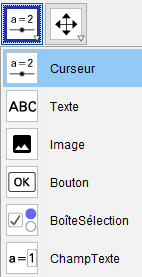
La fenêtre ci-après s’ouvre. Dans le champ de saisie, laisser la lettre du curseur « a » par défaut pour la variable « nombre » et modifier les 3 paramètres « Intervalle » :
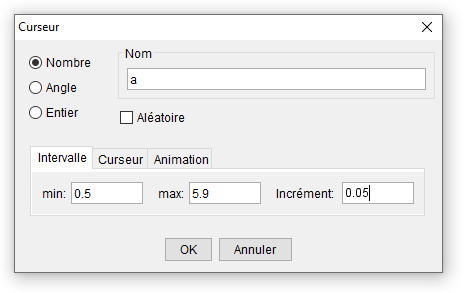
- Le minimum, le fait de choisir la valeur 0.5 permettra ensuite d’avoir les arêtes de la stella octangula de longueur minimale de 0,5 × 2 = 1 cm si on choisit plus loin l’unité « centimètre » ;
- Le Maximum, le fait de choisir la valeur 5.9 permettra ensuite d’avoir les arêtes de la stella octangula de longueur maximale de 5,9 × 2 = 11,8 cm si on choisit plus loin l’unité « centimètre » ;
- L’incrément 0.05 correspond à la précision du demi-millimètre si on choisit plus loin l’unité « centimètre ».
Valider en cliquant sur « OK ».
2. Modélisation d’une enveloppe d’une stella octangula avec GeoGebra classic 5
2. Modélisation d’une enveloppe d’une stella octangula avec GeoGebra classic 5
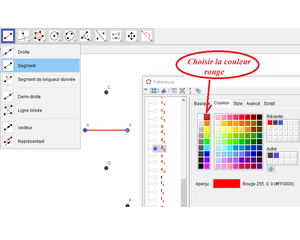
Pour se faire, il s’agit de commencer par tracer un « segment de longueur donnée » a en cliquant sur l’outil des « droites, segments, etc. » puis de sélectionner « Segment de longueur donnée », cliquer dans la fenêtre (un point A se place par défaut), taper « a » et « OK ».
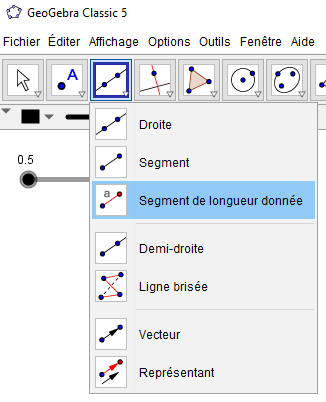
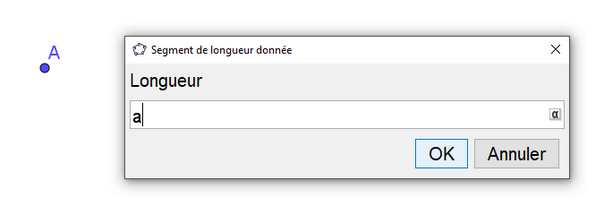
Affichage
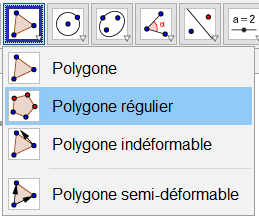
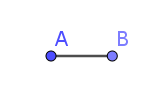 L’enveloppe de la stella octangula n’est constituée que de triangles équilatéraux. Pour en tracer un automatiquement, cliquer sur l’icône Polygone en sélectionnant « Polygone régulier » suivi des clics sur les points A puis B. Ecrire le nombre de sommets « 3 » dans la fenêtre et « OK ».
L’enveloppe de la stella octangula n’est constituée que de triangles équilatéraux. Pour en tracer un automatiquement, cliquer sur l’icône Polygone en sélectionnant « Polygone régulier » suivi des clics sur les points A puis B. Ecrire le nombre de sommets « 3 » dans la fenêtre et « OK ».
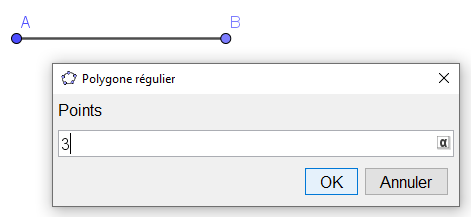
Affichage :
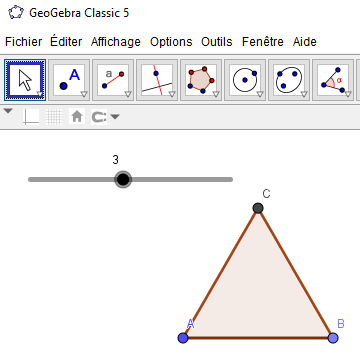
Puis continuer de tracer les autres triangles équilatéraux comme suit afin d’obtenir la plus connue des enveloppes (celle qu’on trouve sur Internet) d’une stella octangula. Enregistrer le fichier sous enveloppe-stella-octangula.ggb puisqu’il servira plus tard.
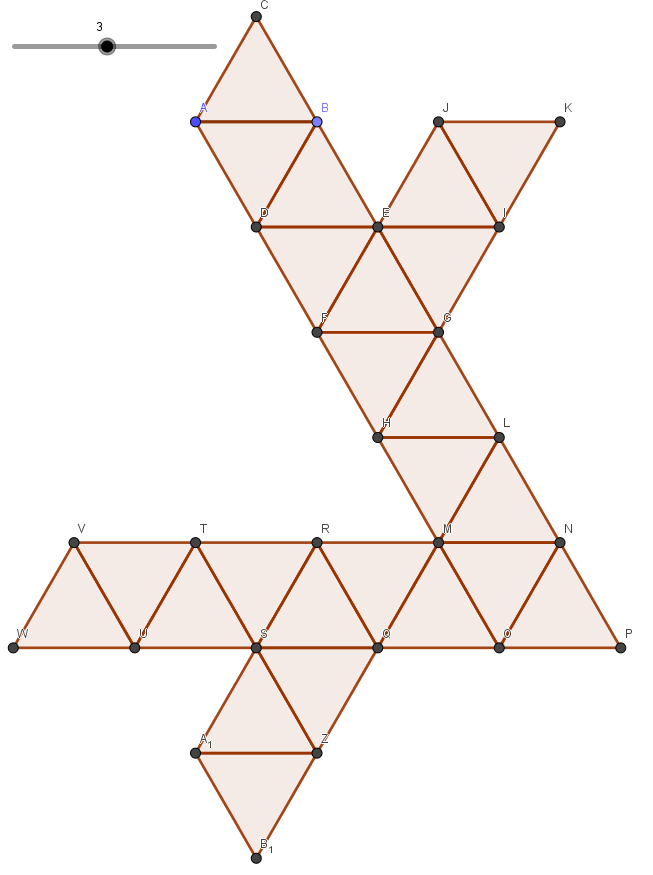
3. De l’enveloppe au patron : des contraintes de chemin, couleur et opacité à respecter dans GeoGebra (utilisation des outils ggt)
Dans cette section, il s’agit de modifier l’enveloppe réalisée dans GeoGebra nommée enveloppe-stella-octangula.ggb afin de respecter deux contraintes :
1) Le chemin : pour que la découpeuse ne découpe qu’une seule fois, il ne doit pas y avoir de superposition de segments ou autres objets mathématiques respectant la contrainte de couleur énoncée au point 2). Si, par exemple, trois segments respectant la contrainte de couleur 2) sont superposés, la lame de la découpeuse passera trois fois à cet endroit.
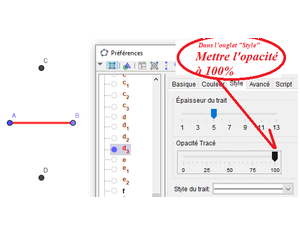
2) La couleur et l’opacité du chemin : par défaut, les découpeuses découperont les lignes rouges RGB(255,0,0) bien opaques dans d’un fichier au format SVG.
Par ailleurs, il faut savoir que les tracés pleins rouges opaques seront découpés en entier et que les tracés en pointillés, puisque découpés en pointillés, peuvent servir à réaliser des pliures faciles dans le papier cartonné.
Modification du fichier GeoGebra pour obtenir un patron découpable par une découpeuse numérique
Ouvrir le fichier enveloppe-stella-octangula.ggb et l’enregistrer sous patron-stella-octangula-sans-colle.ggb
Pour respecter la contrainte énoncée précédemment (deux segments ne doivent pas être superposés), sachant qu’il a été fait plusieurs polygones, il est préférable de cacher tous les polygones et tous les segments en cliquant droit sur l’un des triangles puis « propriétés » puis en sélectionnant d’une part « Polygone » et d’autre part « Segment » et décochant la case « Afficher l’objet » dans l’onglet « Basique » :
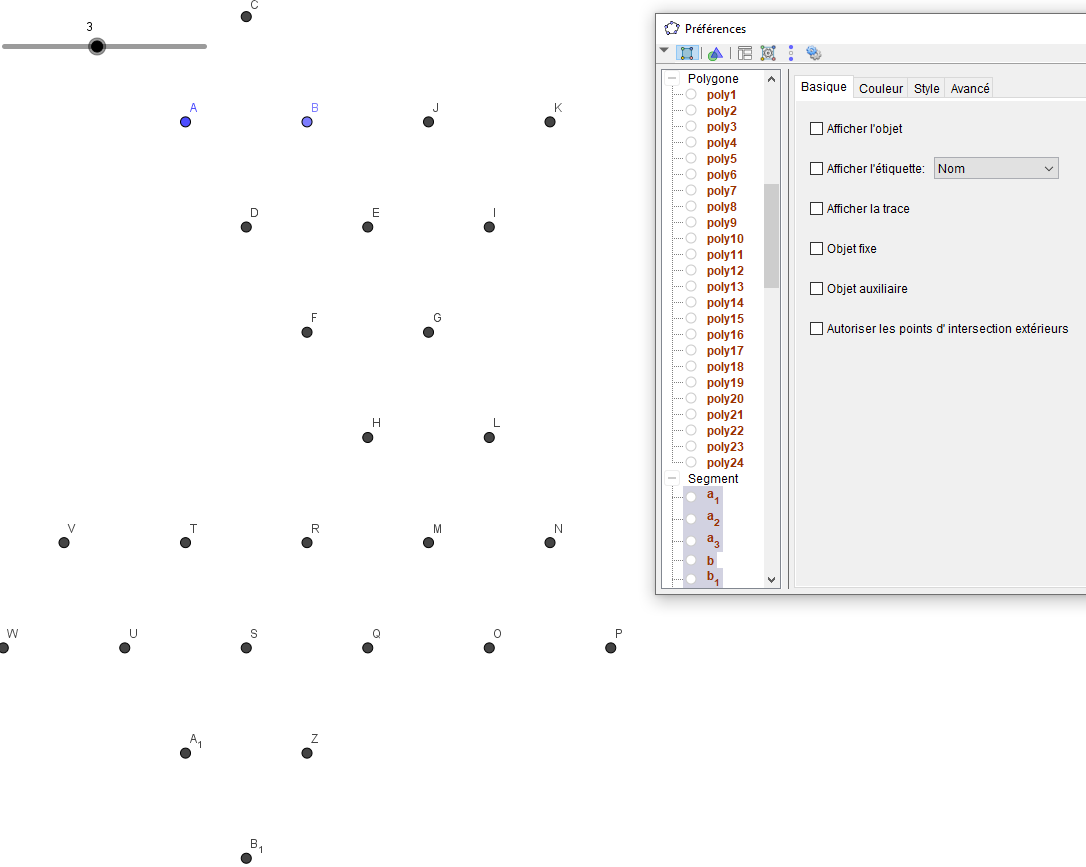
Plutôt que d’avoir à refaire chaque segment et le mettre en rouge opaque comme suit :
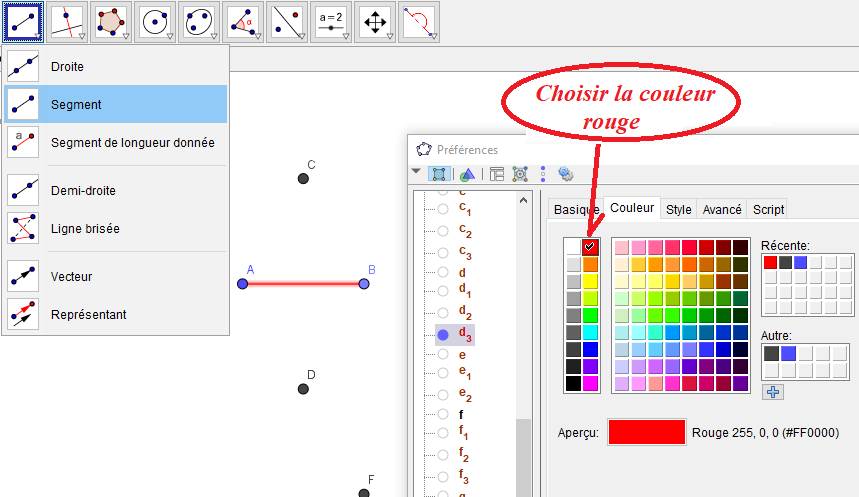

Les outils au format ggt, installés et apparaissant dans la barre personnalisée, vont permettre de placer segments et languettes en cliquant tour à tour sur les points afin d’obtenir le patron suivant :
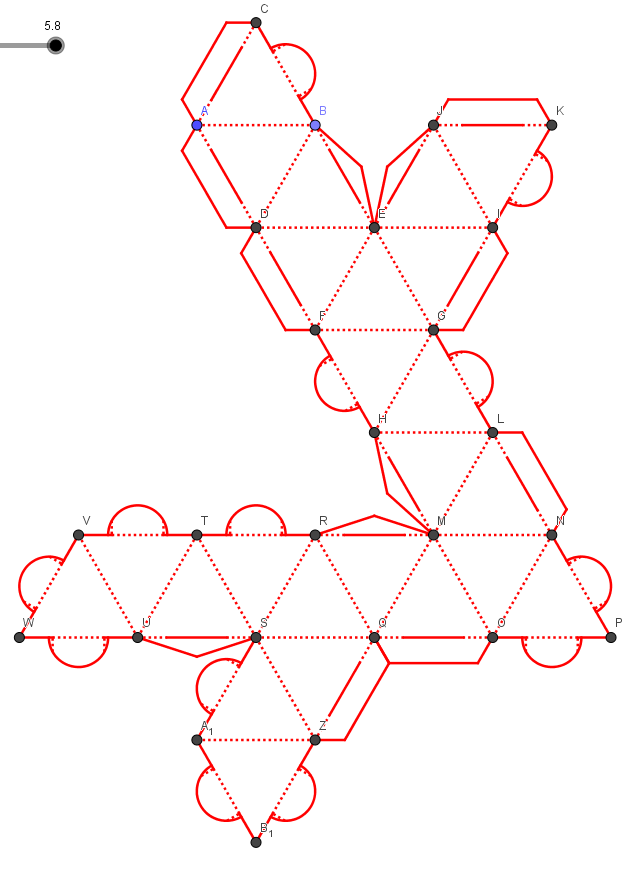
Il ne reste plus qu’à cacher tous les points en cliquant droit sur l’un d’eux, puis « Propriétés », sélectionner « Point » dans la colonne de gauche et décocher la case « Afficher l’objet » dans l’onglet « Basique ».
Pour finir cette étape, afin d’avoir le patron le plus grand possible sur une feuille de format A3 (29,7 cm x 42 cm), le curseur est à positionner sur 5.8 (éventuellement à cacher) ce qui permettra d’avoir une longueur d’arête de stella octangula de 11,6 cm. Ne pas oublier d’enregistrer le fichier GeoGebra patron-stella-octangula-sans-colle.ggb.
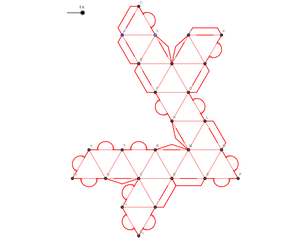
Affichage du patron prêt à être exporté au format SVG :
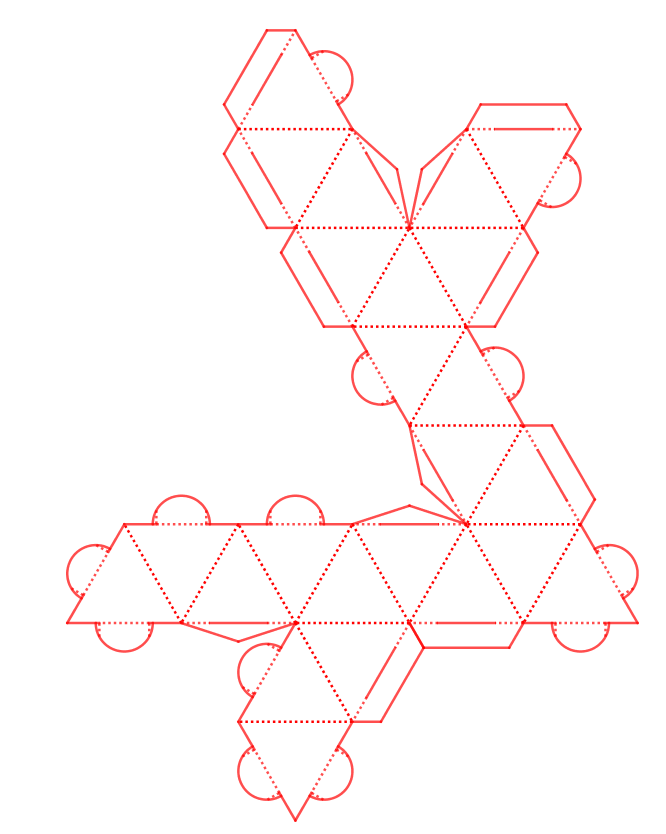
4. Exportation du patron GeoGebra au format SVG et importation vers le logiciel Silhouette Studio Designer ou Business Edition
4.1. Exportation du patron au format SVG
Ouvrir le fichier patron-stella-octangula-sans-colle.ggb si ce n’est pas déjà fait.
Dans l’onglet « Fichier » cliquer sur « Exporter » et « Graphique en tant qu’image (png,eps)… » ou utiliser directement les touche Ctrl+Maj+U.
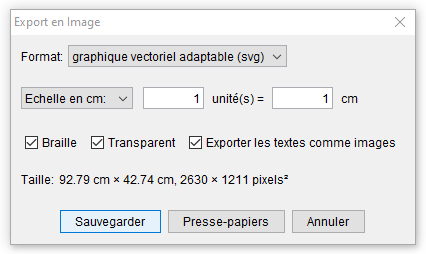
Choisir « Graphique vectoriel adaptable (svg) et l’échelle 1puis sauvegarder sous le nom patron-stella-octangula-sans-colle-a3.svg.
4.2. Importation dans le logiciel Silhouette Studio Designer ou Business Edition
Etapes à suivre :
- Ouvrir le logiciel Silhouette Studio Designer ou Business Edition
- Ouvrir le fichier patron-stella-octangula-sans-colle-a3.svg avec les touches du clavier Ctrl+O ou « Fichier » puis « Ouvrir »
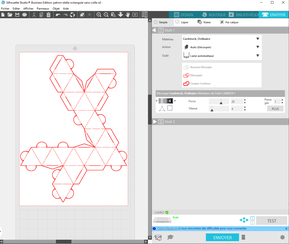
- Afficher la fenêtre de mise en page et régler les paramètres comme sur les copies d’écran suivantes :
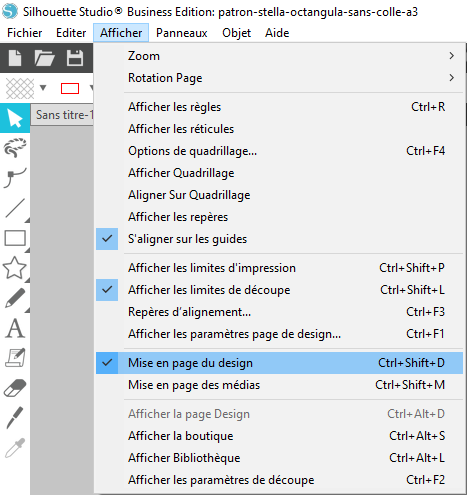
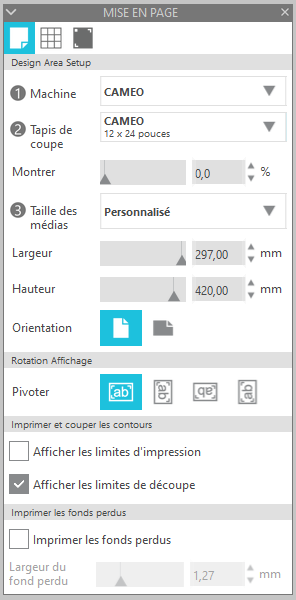
- Ajuster la position du patron sur la page blanche en maintenant appuyé le bouton gauche de la souris pour glisser le patron. Enregistrer le fichier sous patron-stella-octangula-sans-colle-a3.studio3.
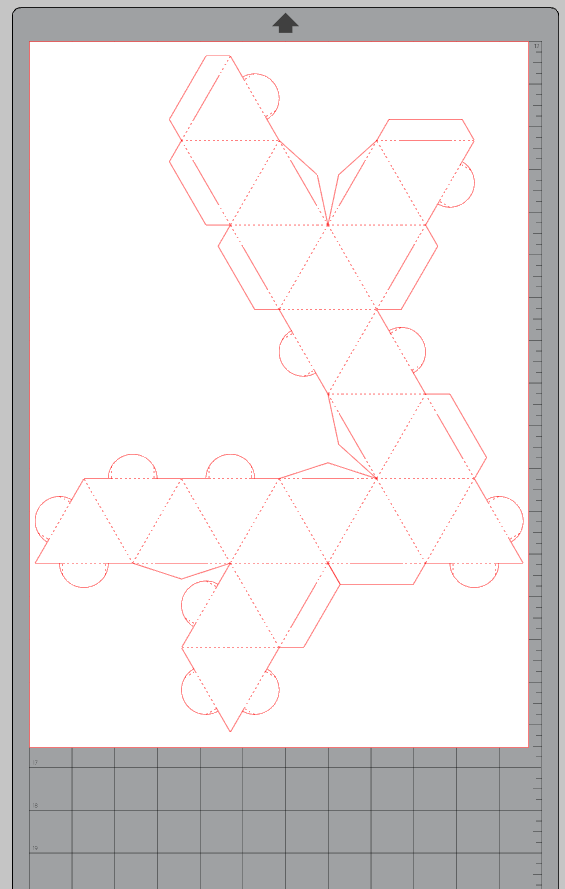
5. Utilisation de la découpeuse Silhouette CAMEO 4
5. Utilisation de la découpeuse Silhouette CAMEO 4

Photographie d’un aménagement dans une salle de classe du collège Les Ormeaux à Rennes : visualiseur numérique, ordinateurs, imprimante 3D et découpeuse numérique à lame.
Etapes à suivre :
- Brancher votre découpeuse Silhouette CAMEO 4 au courant et à votre ordinateur puis placer la feuille de papier cartonnée 160 g/m² au format A3 sur votre tapis de transport (conserver bien à plat le plastique qui protégeait votre tapis) ;

- Allumer votre découpeuse et positionner votre tapis de transport ;

- Charger votre tapis de transport ;

- Dans le logiciel silhouette Studio Business Edition, aller sur l’onglet « Envoyer » qui se trouve en haut à droite ;

- Ajuster les paramètres de découpe. Ci-après, une proposition de ces paramètres ;
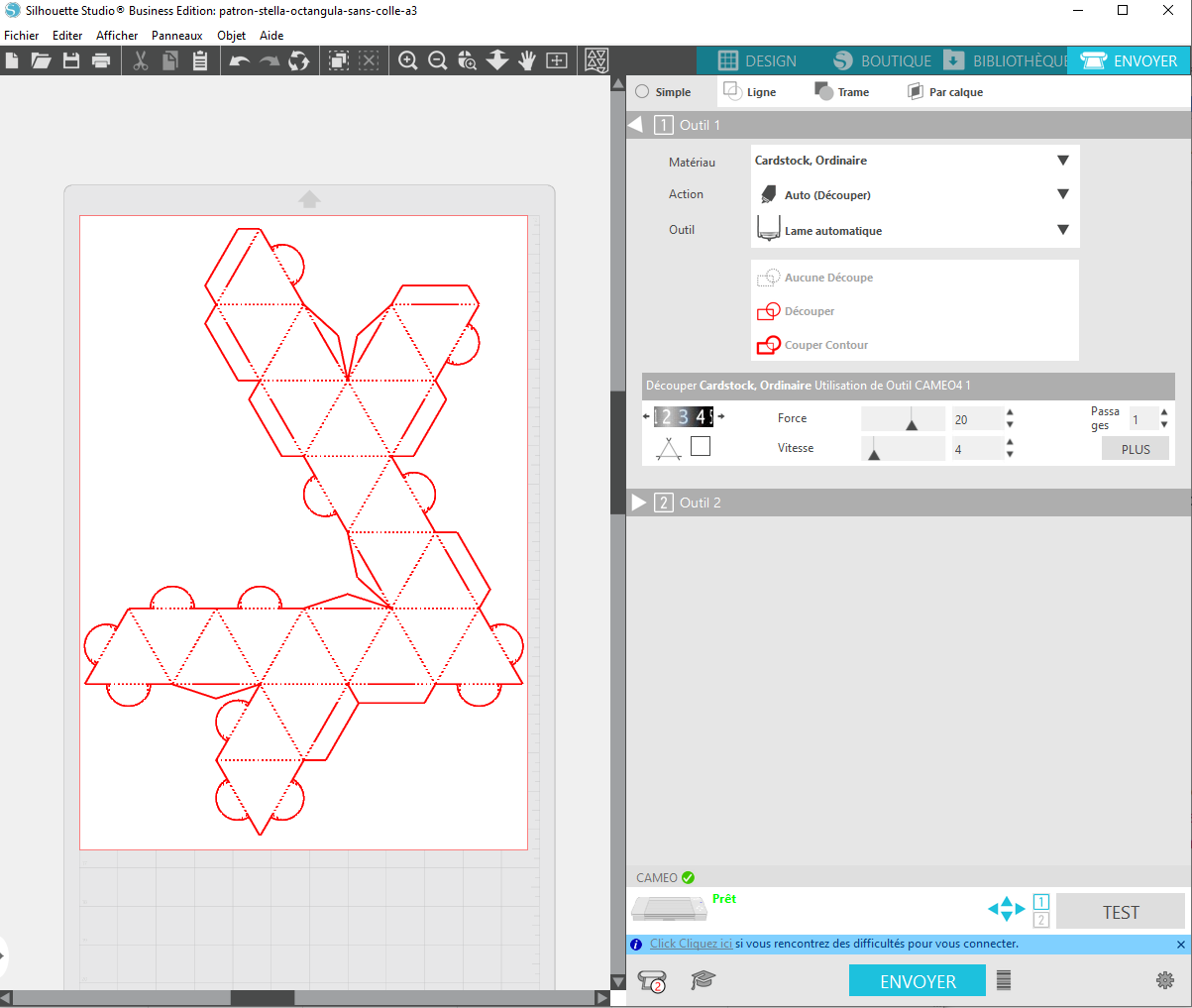
- Cliquer sur « Envoyer » en bas à droite. La découpeuse commence sa découpe ;
- Une fois que la découpeuse s’arrête, appuyer sur le bouton vers le bas pour éjecter le tapis de transport ;

- Pour décoller la feuille de papier du tapis de transport, retourner le tapis (cela évite votre feuille de papier de rouler sur elle-même) et décoller progressivement en vous aidant de vos deux mains ;


- Remettre le film protecteur sur le tapis de transport ;
- Désolidariser le patron du reste de la feuille de papier cartonnée pour obtenir uniquement le patron.

6. Pliage du patron
- Commencer par marquer les plis ;

- Constituer un premier tétraèdre en commençant par le haut du patron, puis un second et ainsi de suite, en veillant bien à « verrouiller » les languettes à l’intérieur en les pliant ;


- Pour les deux dernières languettes, il est préférable de les rentrer toutes les deux en même temps en s’aidant éventuellement d’une paire de ciseaux ;

- La stella octangula terminée :

- Selon votre matériel, taille du tapis de transport, format du papier, colle ou non, il est possible de modifier le curseur dans GeoGebra ainsi que le type de languettes si vous souhaitez utiliser de la colle pour une meilleure finition.
7. Un autre patron pour effectuer une fractale de stella octangula sans colle avec des feuilles A4
7. Un autre patron pour effectuer une fractale de stella octangula sans colle avec des feuilles A4
Il existe plusieurs façons de réaliser une stella octangula en papier cartonné.
Celle énoncée précédemment consistait en la réalisation d’un patron en un seul morceau.
Une autre façon serait de positionner (avec de la colle ou sans) des tétraèdres réguliers sur un octaèdre régulier de longueur d’arêtes égale à celle des tétraèdres.
La façon proposée ci-après consiste à suivre un algorithme
Etape 0 : construire un tétraèdre régulier et repérer le milieu de chaque arête.
Etape 1 : sur chaque face de tétraèdre(s), construire un tétraèdre dont les sommets de sa base sont les milieux repérés à l’itération précédente. Puis repérer le milieu de chaque arête latérale des tétraèdres construits.
En ajoutant les languettes à l’aide de l’outil GeoGebra, on obtient le patron une face de tétraèdre à dupliquer 4 fois et celui d’un petit tétraèdre incomplet (une face en moins) de longueur d’arête la moitié de celle du plus grand à dupliquer 4 fois également.
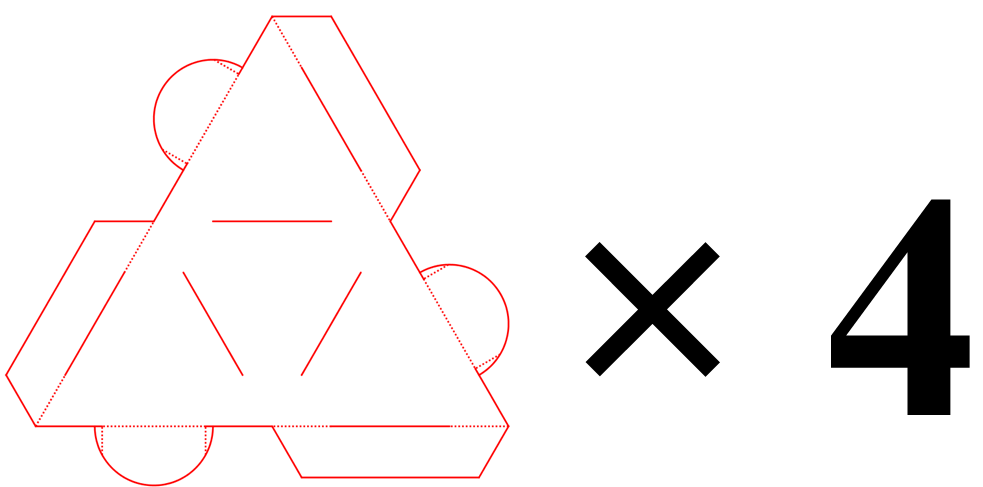

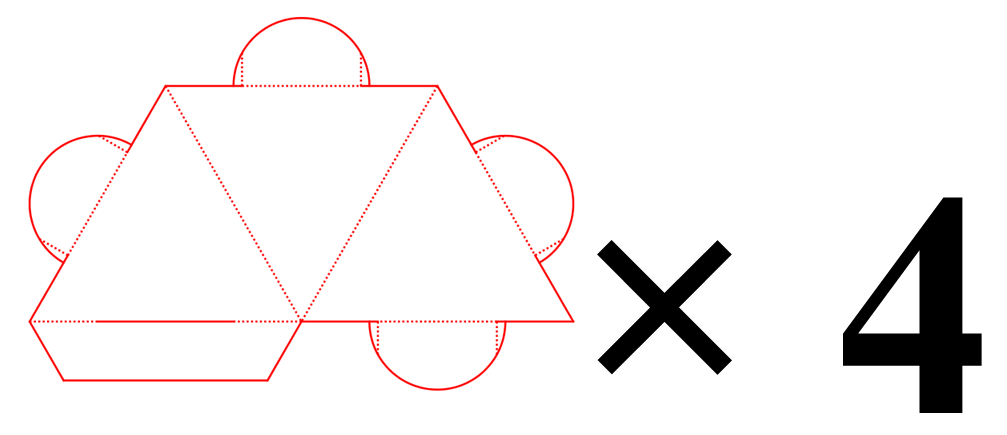

Le verso :

Pour assembler la dernière face, rentrer les 4 languettes en même temps.

Ce qui nous donne une stella octangula.

Vers le patron et la fabrication d’une fractale de stella octangula
Si on reproduit l’étape 1 de l’algorithme encore 2 fois (itération 3), on obtient le patron complet de la fractale de stella octangula dont les morceaux sont, ci-après, rassemblés sur de mêmes pages prêts à être découpés par la Cameo silhouette studio. Les fichiers prêts à l’emploi sont disponibles au téléchargement à la fin de cet article.
Il est préférable d’utiliser du papier cartonné A4 plus épais 350 g/m² pour les plus grands tétraèdres.
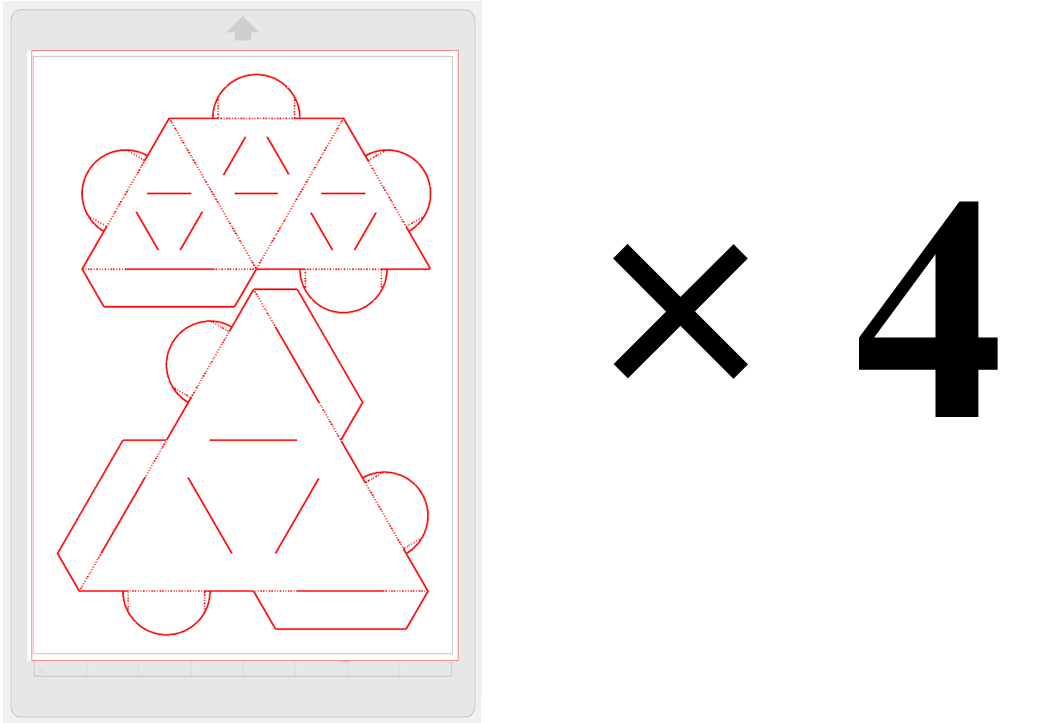
Et du papier cartonné A4 160 g/m² pour les plus petits tétraèdres.

Pour assembler les patrons, il faut commencer par les plus petits tétraèdres et finir par le plus grand.

L’objet final :
La stella octangula et sa fractale sont assez solides comme on peut le voir sur l’image ci-après, puisqu’à deux, elles servent d’étagère.

La réalisation de solides mathématiques peut faire l’objet d’un projet mathématique à part entière : de l’étude du solide à sa réalisation, mais aussi être intégrée à un parcours tel que artistique et culturel (par exemple design).
8. Comment mettre les patrons en couleur ?
8. Comment mettre les patrons en couleur ?
Ouvrir GeoGebra classic 5 et ouvrir le fichier de la figure de l’enveloppe réalisée au point 2 nommée enveloppe-stella-octangula.ggb et l’enregistrer sous patron-stella-octangula-sans-colle-couleur.ggb.
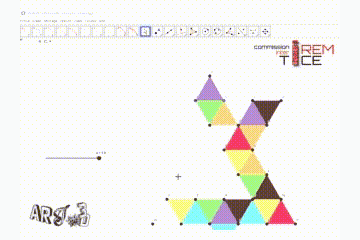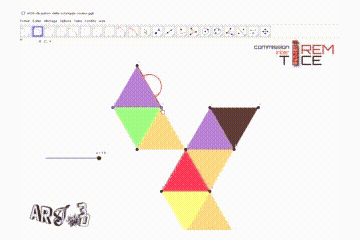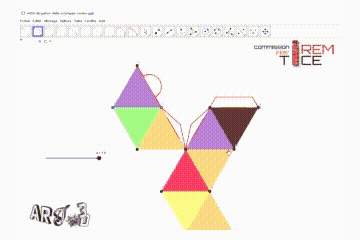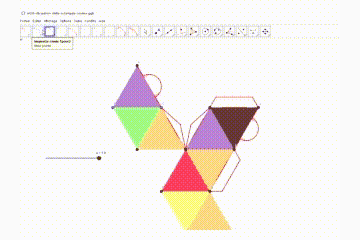
Effectuer les modifications de couleur comme suit en mettant les triangles équilatéraux en couleur et réduisant l’épaisseur de leurs côtés à 0 (dans les propriétés). Pour gagner en rapidité, il est possible d’utiliser l’outil « Copier Style graphique ».
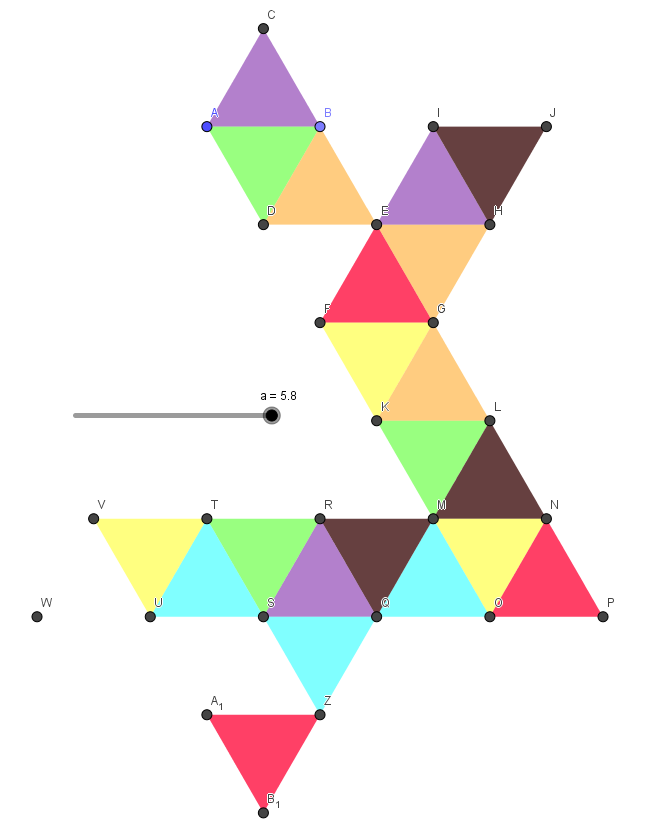
Puis compléter le modèle avec les languettes comme au point 3 précédent pour obtenir un patron et modifier le curseur a = 5 pour que ce nouveau patron puisse tenir sur une feuille A3 dans un nouveau modèle dans le logiciel Silhouette Studio.
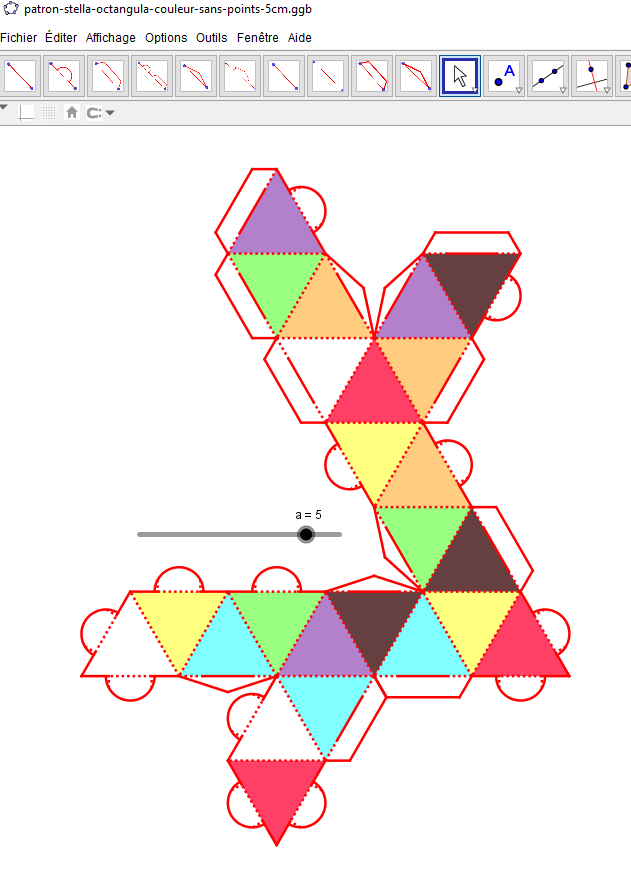
Suivre à nouveau le point 4 précédent pour exporter le patron au format SVG en le nommant patron-stella-octangula-sans-colle-couleur-a3.svg et l’importer dans le logiciel Silhouette Studio Designer ou Business Edition.
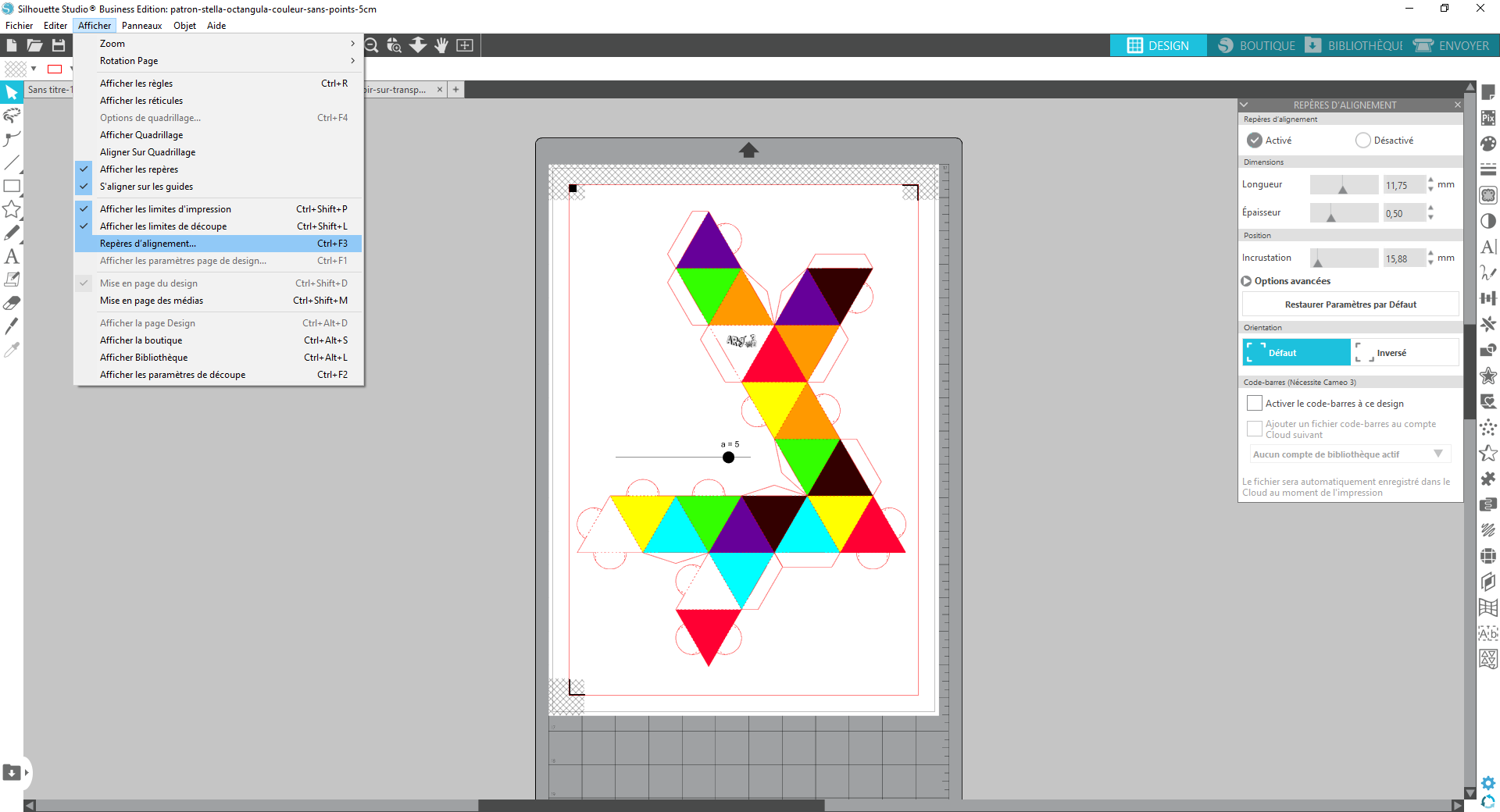
Dans le logiciel Silhouette Studio, activer les « Repères d’alignement ». On peut remarquer que l’espace de découpe est inférieur à celui qui n’utilise pas de couleur, d’où le changement du curseur a = 5.
Bien repositionner le patron à l’intérieur du cadre. Toutes les parties qui se trouveront en dehors du cadre ne seront pas découpées.
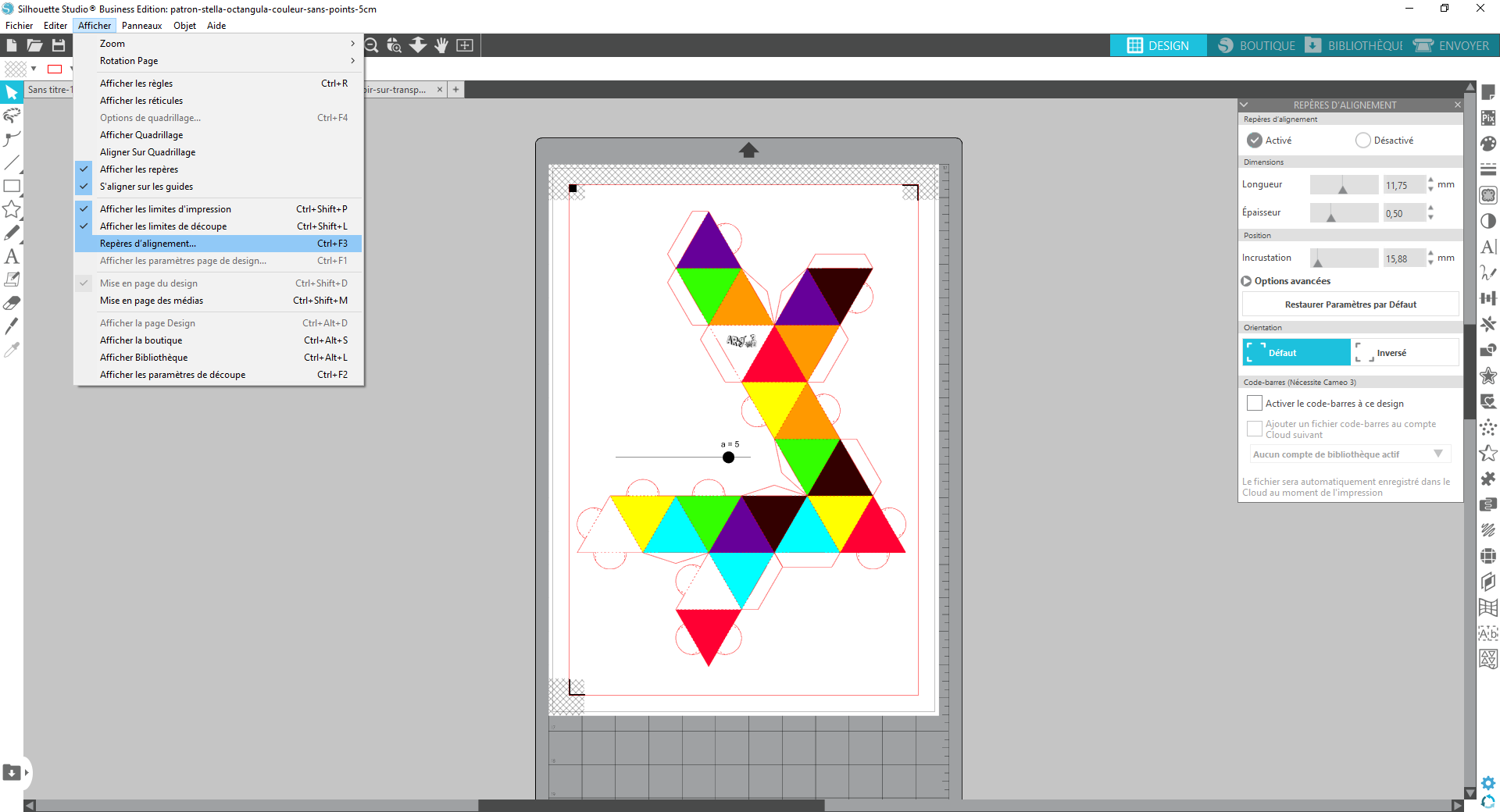
Enregistrer le fichier sous patron-stella-octangula-sans-colle-couleur-a3.studio3.
Imprimer en couleur sur une feuille format A3 à 160g/m² ou 350 g/m². Les languettes ne seront pas imprimées.
Mettre la feuille imprimée sur le tapis de transport de la Silhouette CAMEO 4 en faisant attention de bien la positionner pour que le capteur trouve les repères d’alignement.
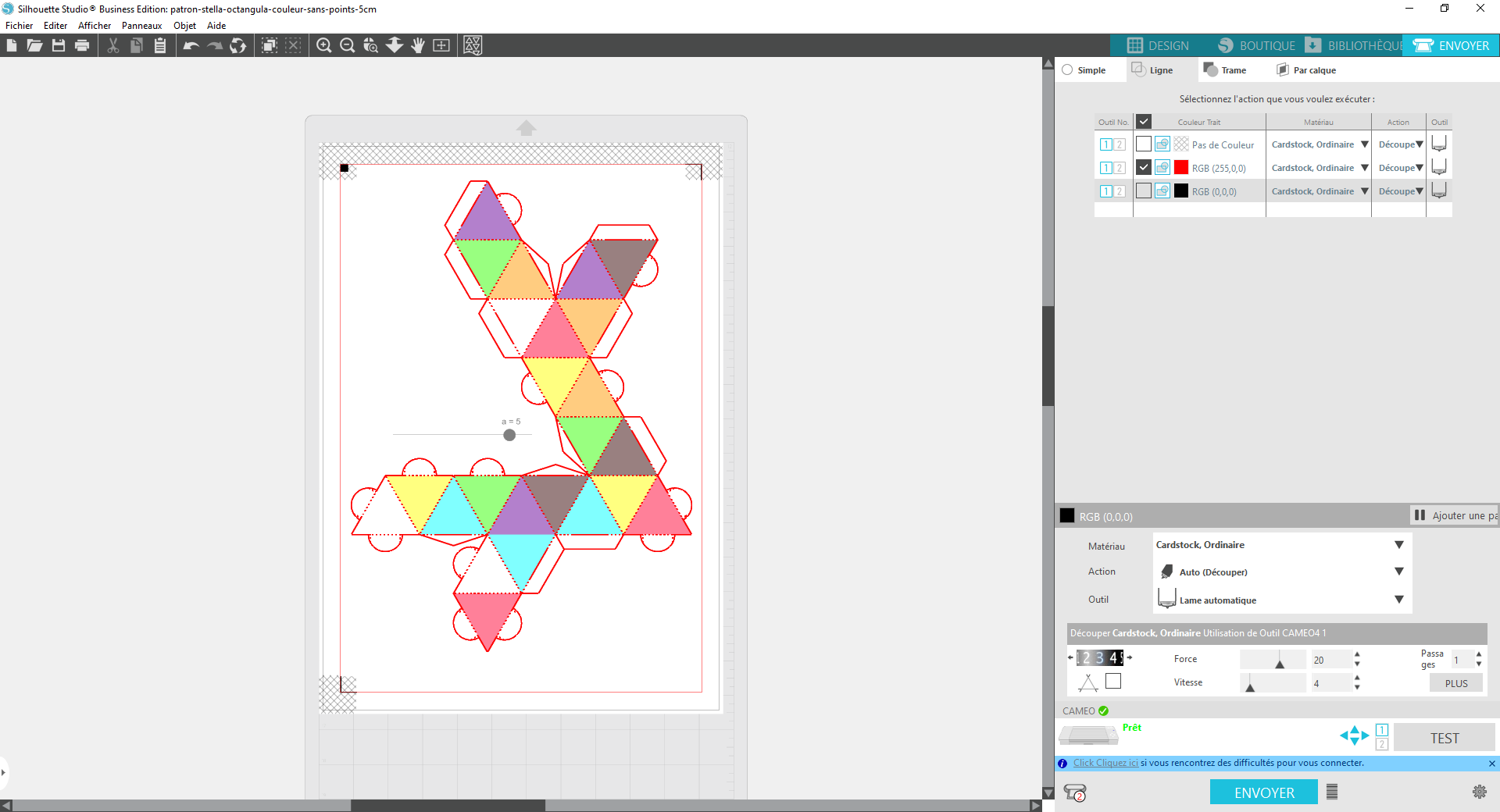
Puis, régler les lignes de découpe (seules les lignes rouges doivent être activées) avant d’envoyer la découpe.
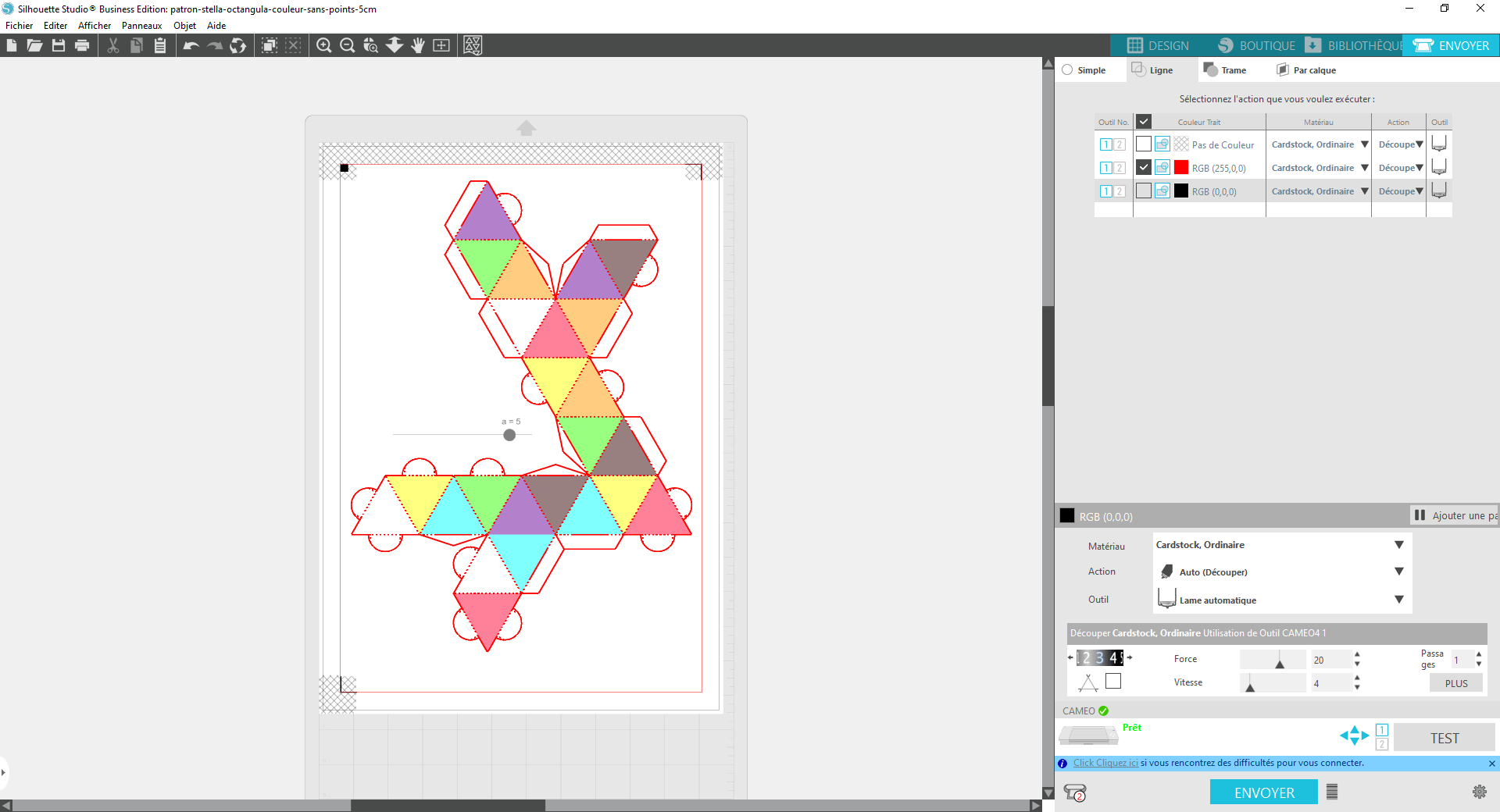
Le patron en cours de découpe :
Le patron découpé :

La stella octangula en couleur assemblée :
Il est ainsi possible de réaliser de nombreux patrons de solides comme ceux mis en téléchargement dans un article de cette même rubrique du site et aussi sur d’autres sites mis en lien à la fin de cet article.
Pour une meilleure précision et solidité, les languettes à coller mises également dans les outils GeoGebra art3d-clb-outils-languettes-decoupeuse-v2021.ggt, sont préconisées.
Galeries










Précédent
Suivant
Téléchargement


Documentation et liens
- Pour en savoir plus sur le contenu des fichiers vectoriels SVG, en lien une vidéo du créateur de Grafikart, développeur freelance Tutoriel SVG : Le format SVG
- Un Tutoriel pour apprendre à utiliser le format SVG de Maurice Chavelli publié sur le site Developpez.com
- Autres articles dans la rubrique FabLab du site C2iT
- Autres articles dans la rubrique GeoGebra du site C2iT
- Pour obtenir plus de modèles de patrons prêts à être découpés sur le site ARt3D
- Le blog de Silhouette France pour obtenir différents tutoriels portant sur la CAMEO 4 ainsi que pour l’utilisation du logiciel Silhouette Studio à acheter en complément. Afin de pourvoir importer et exporter les fichiers SVG, choisir préférablement la version Business Edition